0x520 MLP

1.1. FFN

1.2. Gated Models

Deep models are difficult to train (gradient vanishing). To train efficiently, we want to keep the singular value of Jacobian near 1, explained by this paper

One approach to achieve this is to use the models with gating mechanisms.

Model (residual network)

Model (Highway network)

\[y = H(X)T(X) + X(1-T(X))\]

where the \(T(X)\) is the transform gatew, which controls the behavior of highway layer from the plain layer \(H(X)\) or identity layer \(X\)

• when \(T(X)=1\), \(y=H(X)\)
• when \(T(X)=0\), \(y=X\)

The transform gate can be implemented as follows:

\[T(X) = \sigma(WX+b)\]

where \(\sigma\) is sigmoid and \(b\) should be a negative value to initially bias towards the identity layer

Model (Gated Linear Unit, GLU) take element-wise product with a sigmoid function to control activation

\[h(X) = (XW+b) \cdot \sigma(XV + c)\]

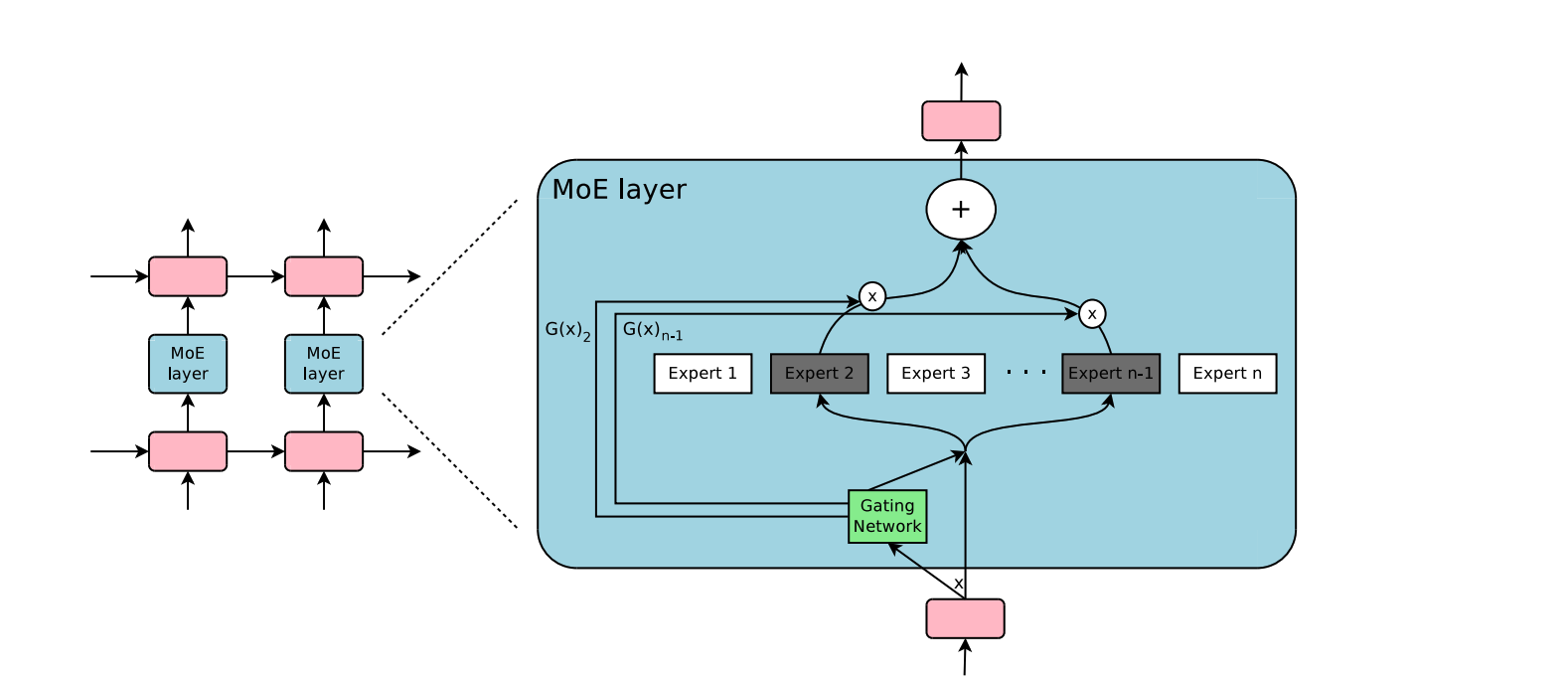
Model (sparsely-gated mixture of experts) experts can be more than thousands

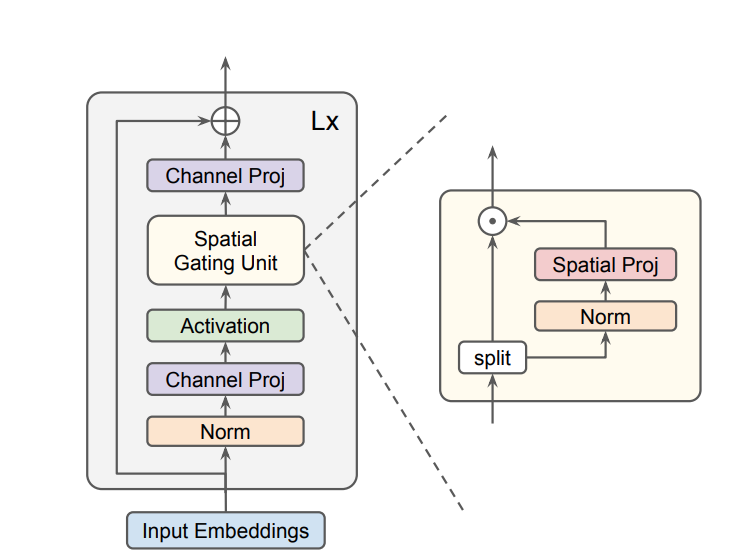
Model (gMLP, MLP with gating): self-attention is not always necessary depending on the task. MLP might be enough

First we have a channel projection (linear projection) and activation.

\[Z = \sigma(XU)\]

Then we model the spacial interaction \(s\)

\[\tilde{Z} = s(Z)\]

If \(s\) is identical, the entire operation is reduced to FFN. This work uses Spatial Gating Unit which first splits \(Z\) into \((Z_1, Z_2)\)

\[f(Z_2) = WZ_2+b\]

\[\tilde{Z} = Z_1 \circ f(Z_2)\]