0x301 Complexity
Complexity zoo has a good explanation for each of the complexity classes.
1. Asymptotic Analysis
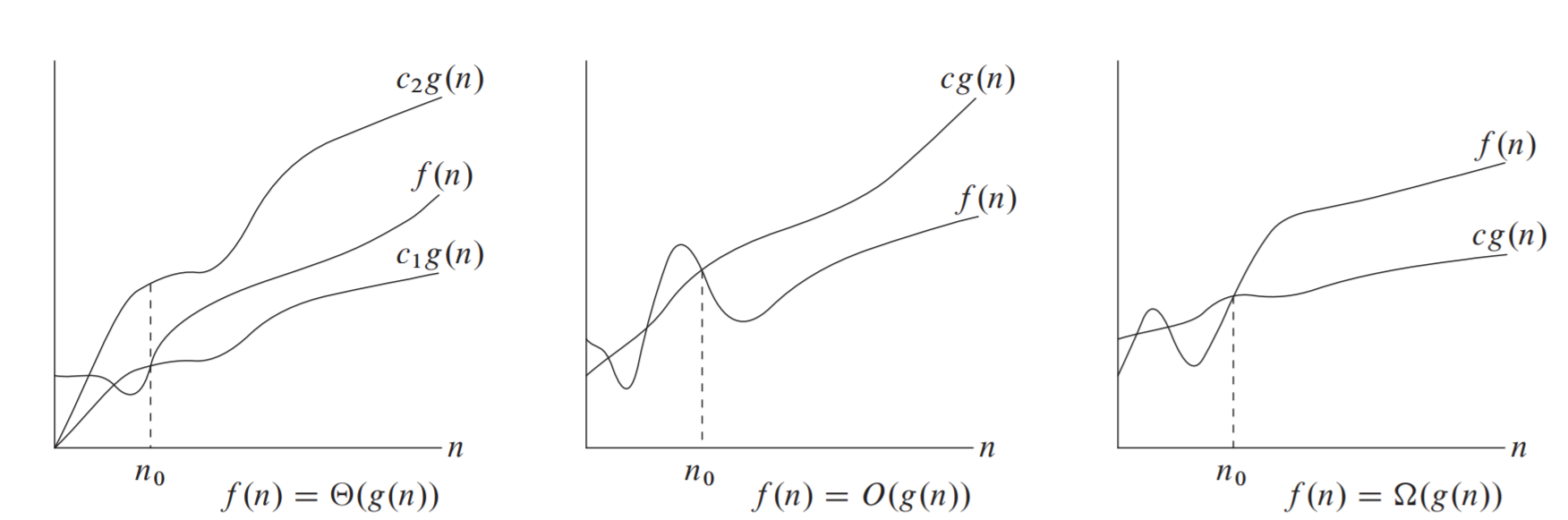
Definition (\(\Theta\)-notation) For a given function \(g(n)\), we denote by \(\Theta(g(n))\) the set of functions
We say that \(g(n)\) is an asymptotically tight bound for \(f(n)\), it bounds the function from above and below
Definition (O-notation) For a given function \(g(n)\), we denote by \(O(g(n))\) the set of functions
This is an asymptotic upper bound.
Definition (\(\Omega\)-notation) For a given function \(g(n)\), we denote by \(\Omega(g(n))\) the set of functions
This is an asymptotic lower bound.
Theorem (notation relations) For any two functions \(f(n), g(n)\), we have
2. Time Complexity
Definition (time complexity) Let \(M\) be a deterministic Turing machine that halts on all inputs. The time complexity of \(M\) is the function \(f: \mathcal{N} \to \mathcal{N}\) where \(f(n)\) is the max number of steps that \(M\) uses on any input of length \(n\)
- P: decidable in polynomial times
- NP: verifiable in polynomial times
- co-NP: complement is NP
- NP-complete: A NP problem is NP-complete if any NP can be reduced to this problem in polynomial times
- NP-hard: A problem
if NP-hard if any NP can be reduced to this problem in polynomial times - EXPTIME: decidable in exponential time
Theorems:
- Cook-Levin: Any NP problems can be reduced in polynomial times to Boolean satisfiability problem (Boolean satisfiability is NP-complete)
3. Space Complexity
Definitions
- PSPACE: decidable using polynomial space
- NPSPACE: verifiable in polynomial space
Theorems:
- Savitch: NPSPACE can be reduced to PSPACE (with square space complexity bound)
4. Quantum Complexity
Definitions
- BQP: decidable by quantum computer in polynomial time within ⅓ error probability.
Reference
- [1] Introduction to Algorithm
- [2] Introduction to the Theory of Computation
