0x220 ISA
- 1. History
- 2. Basic
- 3. Arithmetic
- 4. DEC family
- 5. Intel family
- 6. MIPS
- 7. ARM family
- 8. RISC-V
- 9. Nvidia family
- 10. Reference
- 11. Reference
1. History
1950 - 1960
- Traitorous eight left Shockley's lab on 1957, found Fairchild semiconductor
- 1957 development of planar process by Jean Hoerni. 1958, invention of IC (hybrid IC on germanium) by Jack Kilby (Texas Instrument), improved (monolithic IC on silcon) by Robert Noyce (Fairchild).
1960 - 1970 (3rd Generation: IC)
- 1968, Noyce, Gordon left Fairchild and found Intel
1970 - 1980 (4th Gen: microprocessor 10 micro - 1 micro)
2000 - 2010 (50nm - 100 nm)
- Intel released Pentium 4 series, whose strategy then was to improve clock frequency in a single core, which causes much higher power consumption and heat due to leakage.
- AMD introduced Athlon 64 to shift to 64 bit and focused on efficiency in each clock cycle successfully.
- To compete with AMD, Intel switched to Core 2 series whose sales was better than AMD Phenom series. (Interestingly, AMD stock price dropped significantly after Core 2 release)
2010 - Now (10nm -50 nm)
- Intel Core series started tick-tock strategy to improve the manufacturing process and microarchitecture alternatively each year until Skylake. (Nehalem/Westmere, Sandy Bridge/Ivy Bridge, Haswell/Broadwell, Skylake)
- AMD acquired ATI in 2006 and improved its graphic performance.
- On GPU side, AMD Radeon 4000 compete with NVIDIA Geforce 200 successfully, but on CPU side, AMD announced Bulldozer (FX series) to compete with Intel Core series. The CPU side was not successful until Zen series.
2. Basic
Instruction Processing Style
- 0-address: stack machine (op, push A, pop A)
- 1-address: accumulator machine (op ACC, ld A, st A)
- 2-address: 2-operand machine (op S,D; one is both source and dest)
- 3-address: 3-operand machine (op S1, S2, D; source and dest separate)
Stack machine
Advantages are the small instruction size and efficient procedure calls (all params are on stack so no additional cycles for parameter passing)
Downsides are computations that are not easily expressible with postfix notation are difficult to map to stack machines
Not that stack machine is a class of pushdown automaton, therefore not Turing complete. If it has two stacks, It is equivalent to Turing machine.
Data Types
Representation of information for which there are instructions that operator on the representation
Example: integer (two endians), float point, char, binary . Some rare examples are queue, doubly linked lists, and even objected oriented (intel 432) !
Memory Organization
Address space: How many uniquely identifiable locations in memory
Addressability: how much data does each uniquely identifiable location store
- bit addressable: Burroughs B1700 (purpose of this was to virtualize ISA)
- byte-addressable: most ISA
- 64-bit addressable: some supercomputer
- 32-bit addressable: first Alpha
Support for virtual memory
Registers More vs Less
benefit or more registers: enable better register allocation by compiler
benefit of fewer registers: save number of bits for encoding register address, small register file.
Addressing Mode
Addressing modes specify how to obtain the operands
- Absolute: use the immediate value as address (e.g: LW rt, 10000)
- Register Indirect: use GRP[r_base] as address (e.g: LW rt, (r_base)
- Displaced or based: use offset + GPR[r_base] as address (LW rt, offset(r_base))
- Indexed use: GPR[r_base] + GPR[r_index] as address (LW rt, (r_base, r_index))
- Memory Indirect: use value at M[GPR[r_base]] as address (LW rt((r_base))
- Auto inc/decrement: use GRP[r_base] as address but inc or dec (LW rt, (r_base))
More addressing modes
- The good point is that it enables better mapping of high-level constructs to the machine such as array, pointer-based accesses. (e.g: array access can be implemented with auto inc).
- The downside is hard to design and too many choices for compiler.
RISC vs CISC
- RISC: simple instruction, fixed length, uniform decode, few addressing mode
- CISC: complex instructions, variable length, non-uniform decode, many addressing mode
3. Arithmetic
3.1. Integer
3.2. Real Numbers
Note that historically, floating point is not the only representation for real numbers, there were fixed point representations where the gaps are all of the same size
3.2.1. Fixed-point Representation
Proposed by William Kahan (Turing 1989), as an effort to design intel 8087.
3.2.2. Float Representation
The IEEE 754 standard defines the representation of floating point as follows
The part of \(1+Fraction\) is also called significand, the fraction is also known as mantissa
Representations are different depending on the values of exponential
1. normalized case when exponent are not all zero or all one
where \(bias=2^{k-1}-1\)
2. denormalized case when exponent are all zero, then
Notice both significant and exponent part have changed. This representation has a smooth transition from the denormalized case into normalized case. Additionally it provides a way to represent 0 (actually two way +0.0, -0.0 depending on the sign)
3. special case when exponent are all 1
- if fraction is 0, it is infinity
- otherwise fraction are nonzero, it is NaN
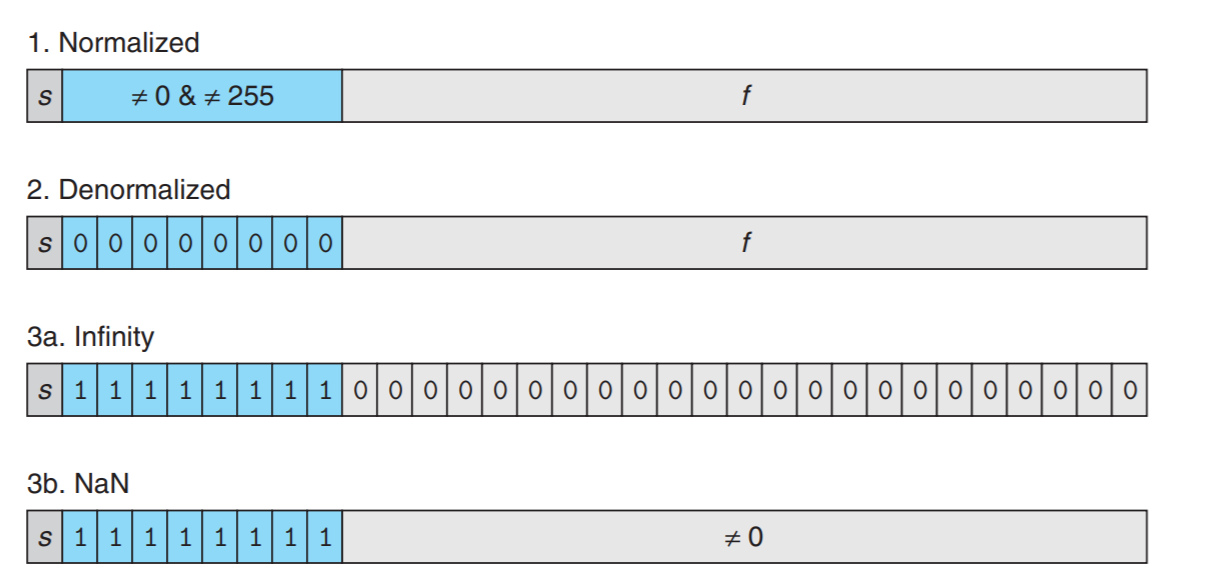
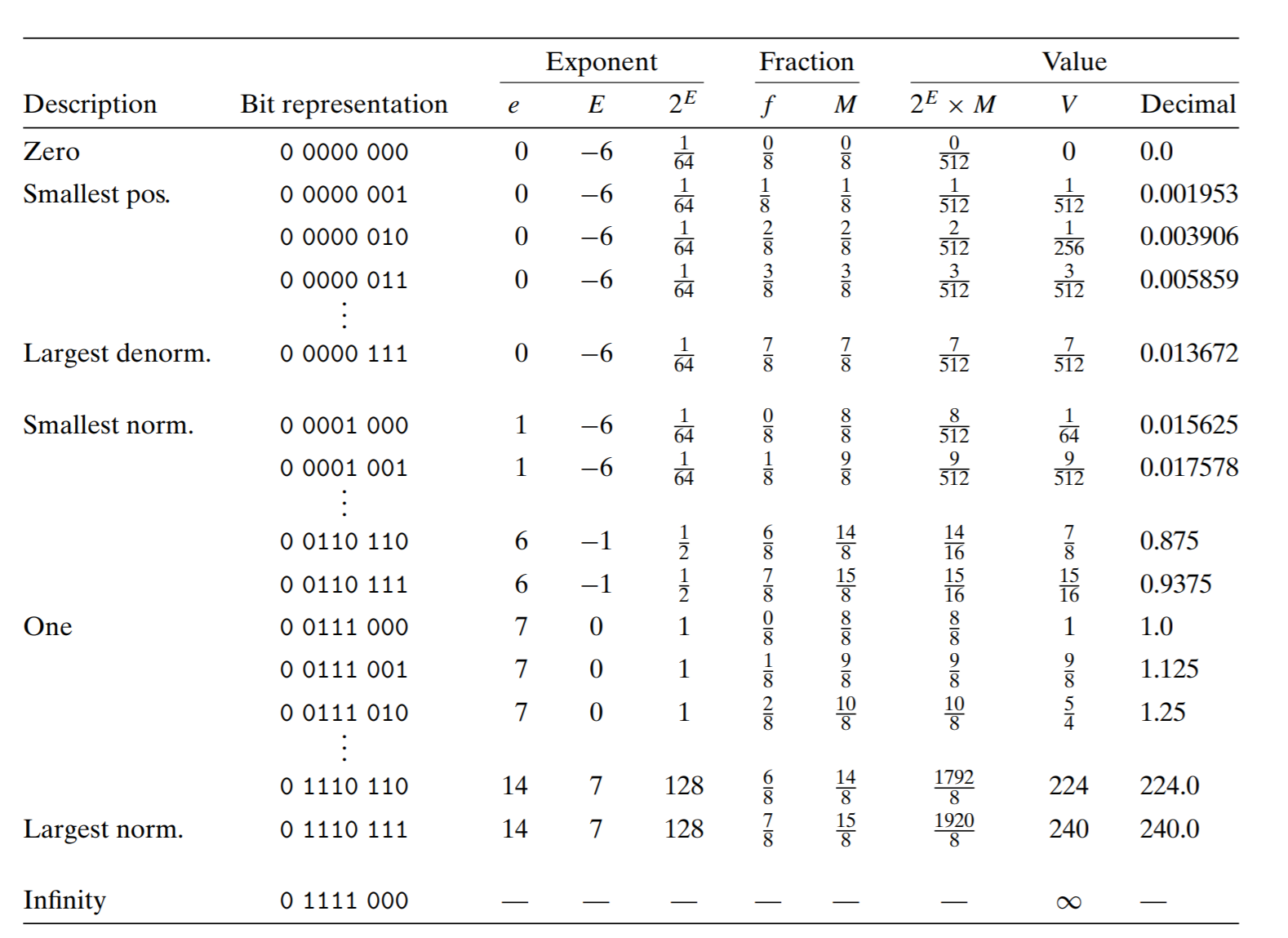
8 bit float number
exponent 4 bit, fraction 3 bit example from CSAPP
single-precision
float
- S is 1 bit
- Exponent is 8 bit and Bias is \(127_{Ten}\)
- Fraction is 24 bit (6 decimal digits of precision)
- range is around \([2.0 \times 10^{-38}, 2.0 \times 10^{38}]\)
var f float32 = 16777216 // 1<<24
fmt.Println(f == f+1) // true
double-precision
In double-precision
- S is 1 bit
- Fraction is 11 bit and Bias is \(1023_{Ten}\)
- Fraction is 52 bit (15 decimal digits of precision)
- range is around \([2.0 \times 10^{-308}, 2.0 \times 10^{308}]\)
To find the detailed numbers on each machine, you can consult
3.2.2.1. Rounding
IEE754 use the Round-to-Even as the default mode.
- It in general rounds to the nearest number
- when the target is at the half of two numbers (e.g: \(XXX.YYY1000\)), then it rounds so that the least significant bit is even (0).
Other possible roundings are
- round toward zero
- round up
- round down
4. DEC family
4.1. PDP
4.2. VAX
4.3. Alpha
5. Intel family
Reference: Intel Manual
5.1. History
- 4004(4bit)
- 8080(8bit)
- 8086(16bit)
- 386(32bit)
- 486
- pentium
- intel64(64bit)
5.2. General Purpose Register
- rax, rbx, rcx, rdx ... r8 ... r15
5.3. Segmentation Register
I found that they are rarely used in recent desktop OS because segmentation has been replaced by paging,
- cs, ds ...
- cs: code
- ds: data
- es: extra
- fs: general purpose
- gs: general purpose
- ss: stack segment
5.4. Control Register
CR0
- PE (0 bit): protected mode enabled
- PG (31 bit): paging unit (CR3) enabled
CR3
- page table based register
5.5. SIMD Register
- xmm0 ... xmm7 (each has 128bit for SSE)
5.6. Arithmetic Instruction
- expensive arithmetic instruction such as multiply and division are only available at rax
5.7. SIMD Instruction
- MMX, SSE, SSE2, SSE, AVX, AVX512
5.8. System call
- sysenter: fast level 3 to level 0 rountine. stack need to store some registers before entry
6. MIPS
Instruction Format
R-type
I-type
J-type
7. ARM family
7.1. License
Arm's license looks interesting. Basically it runs two types of license
- Architecture license just license their ISA
- Cortex license is about their microarchitecture and of course ISA
7.2. A32 Architecture
ARMv3 -> .... -> ARMv7 -> ARMv8 (support for 64bit)
Current processors are named in the format of Cortex-(A|R|M)[0-9]+ where A is for server, R for realtime system, M denotes microcontroller.
7.2.1. A32 Registers
- R0 - R12: general purpose
- SP (R13): stack pointer
- LR (R14) link register
- PC (R15) program counter
7.2.2. A32 Assembly
7.2.3. Thumb Assembly
7.3. A64 Architecture
7.3.1. A64 Registers
- X0-X30: 64bit general purpose
- W0-W30: 32bit general purpose
- ZXR, WZR: zero register
- LR(X30): link register
- SP: stack pointer
- PC: program counter
7.3.2. A64 Assembly
svc for system call
8. RISC-V
9. Nvidia family
PTX
10. Reference
[1] CMU 15418 http://www.cs.cmu.edu/~418/
[2] Hennessy, John L., and David A. Patterson. Computer architecture: a quantitative approach. Elsevier, 2011.
[3] Patterson, David A., and John L. Hennessy. Computer Organization and Design ARM Edition: The Hardware Software Interface. Morgan kaufmann, 2016.
[4] arm developer document https://developer.arm.com/docs
11. Reference
[1] The Computer Book