0x302 Information Theory

Foundation

Information Theory is concerned with representing data in a compact fashion, the most important concepts are summarized here

Definition (entropy) The entropy of a discrete random variable \(X\) with distribution \(p\) is

\[H(X) = -\sum_{k=1}^K p(X=k) \log_2 p(X=k)\]

For a K-ary random variable, the maximum entropy is \(H(X) = \log K\) when \(p(X=k) = 1/K\)

Definition (differential entropy) The continuous version is the differential entropy.

\[H(X) = - \int_{\mathcal{X}} f(x)\log f(x) dx\]

Note this differential entropy is not the exact generalization of the discrete version, the actual generalization is called LDDP

entropy of Gaussian

For a univariate Gaussian variable

\[x \sim \mathcal{N}(\mu, \sigma^2)\]

then its entropy is

\[H(X) = \frac{1}{2}(1 + \log (2\pi\sigma^2))\]

For a multivariate Gaussian variable,

\[x \sim \mathcal{N}_D(\mathbf{\mu}, \mathbf{\Sigma})\]

then its entropy is

\[H(X) = \frac{D}{2}(1 + \log(2\pi)) + \frac{1}{2}\log|\mathbf{\Sigma}|\]

Definition (relative entropy, KL divergence) One way to measure the dissimilarity of two probability distribution \(p, q\) is the Kullback-Leibler divergence (KL divergence) or relative entropy

\[KL(p||q) = \sum_k p_k \log\frac{p_k}{q_k} = -H(p) + H(p, q)\]

KL divergence is the average number of extra bits needed to encode the data \(p\) with distribution \(q\).

Definition (cross entropy) \(H(p,q)\) is called cross entropy, it is to measure the average number of bits to encode data of distribution \(p\) using codebook of distribution \(q\), it is defined as

\[H(p, q) = -\sum_k p_k \log q_k\]

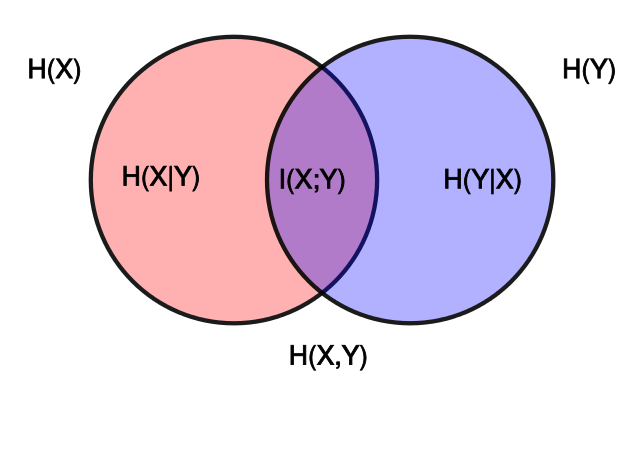
Definition (conditional entropy) The conditional entropy \(H(Y|X)\) is defined as

\[H(Y|X) = -\sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)}\]

It can be re-written as:

\[H(Y|X) = \sum_x p(x) H(Y|X=x)\]

Definition (mutual information) Mutual information or MI is an approach to estimate how similar the joint distribution \(p(X,Y)\) can be factored into \(p(X)p(Y)\)

\[I(X;Y) = KL(p(X,Y)||p(X)p(Y)) = \sum_x \sum_y p(x,y)\log \frac{p(x,y)}{p(x)p(y)}\]

Obviously, MI is zero iff two random variables are independent.

MI can be expressed using entropy as follows

\[I(X;Y) = H(X) + H(X) - H(X,Y) = H(X) - H(X|Y)\]

example of Gaussian

Let \((X,Y)\) be 0 mean and \(\rho\) correlation, then its mutual information is

\[I(X;Y) = h(X) + h(Y) - h(X,Y) = -\frac{1}{2}\log(1-\rho^2)\]

Therefore, MI can be interpreted as the reduction in uncertainty about \(Y\) after observing \(X\)

Statistics based on MI might capture nonlinear relation between variables that can not be discovered by correlation coefficients.

Model (mutual information neural estimator) Estimating mutual information is not easy, it can be done using neural network by optimizing

\[\widehat{I(X;Z)} = \sup_{\theta} E_{P^{(n)}_{XZ}}[T_\theta] - \log(E_{P^{(n)}_X \otimes P^{(n)}_Z}[e^{T_\theta}])\]

using samples of \((x,z)_n\). It is justified by the

Definition (pointwise mutual information) A related concept is pointwise mutual information or PMI, this is about two events \(x,y\)

\[PMI(x,y) = \log \frac{p(x,y)}{p(x)p(y)}\]

Reference

[1] Cover, Thomas M., and Joy A. Thomas. Elements of information theory. John Wiley & Sons, 2012.