0x413 Reinforcement Learning

1. Foundation
- 1.1. Bandit Problem
- 1.2. Reinforcement Learning
2. Dynamic Programming (Model-based)
3. Monte Carlo Methods
4. Temporal-Difference Learning

This note is mostly about tabular methods from Part 1 of Sutton's textbook (Sutton and Barto, 2018)¹ and David Silver's UCL lecture (Silver, 2015)²

1. Foundation

\[\text{Multi-arm Bandit Problem} \subset \text{Contextual Bandit Problem} \subset \text{RL (MDP)}\]

1.1. Bandit Problem

Bandit problems can be considered as a simplification of MDP. They are stateless problems where each arm has a fixed distribution of rewards regardless of previous actions.

1.1.1. Multi-arm Bandit

Suppose we play a game in $n$ rounds, at each round $t$, player chooses an action $A_t=a$ from a finite set of possible choices called arms $\{ 1, ..., m \}$, and the corresponding reward as $R_t$. The value of an arbitary action $a$, denoted $q_*(a)$ is the expected reward

\[q_*(a) = \mathbb{E}[R_t|A_t = a]\]

which is unknown to us, otherwise it is a trivial problem.

We denote the estimated value of action $a$ at timestep $t$ as $Q_t(a)$, which we would like to be close to $q_*(a)$

At the end of each turn $t$, we can estimate the empirical mean reward of arm $a$ by

\[Q_t(a) = \frac{1}{T_a(t-1)}\sum_{s=1}^{t-1}R_a(x)\mathbf{1}_{I_s = a}\]

where $T_a(t-1)$ is the total number that action $a$ has been played.

where $q_*(a)$ is the expected payoff of action $a$, and $q_*$ is the expected payoff best arm.

Applications of multi-armed bandit

There are many applications for multi-armed bandit, for example NY Times uses it to determine which news to show. It can be considered as an alternative to massive AB testing, to test many alternative options at the same time (instead of doing it pairwise)

1.1.2. Contextual Bandit

There is also a generalization of bandit problem called contextual bandit which have access to (state-like) contexts.

Definition (contextual bandit) At each round,

a context (i.e. some clues to states) is selected and revealed to agent
agent has to choose an action based on the context.
environment reveals a reward

Unlike full MDP, there is no transition between states. future states are not affected by user's action, they are independent across each round

Application of contextual bandit

In online news recommendation, we can select news to user based on user's context (e.g. location, browser, history, reading habits...)

1.1.3. Algorithms

Our goal is to minimize the regret

\[\sum_{t=1}^n \sum_{a=1}^m [q_* - q_*(a)] \mathbf{1}_{I_s = a}\]

Algorithm ($\epsilon$-greedy) With probability $\epsilon_t$, play an arm randomly, otherwise select the "best" arm found so far

There are many works to show the regret bound of this algorithm, it is at most logarithmic in $n$.

Paper (regret bound, Lai, Robbins 1985) the optimal machine is played exponentially more often than any other machine asymptotically.

For any suboptimal machine $j$, we have

\[E[T_j(n)] \leq (\frac{1}{D(p_j || p^*)} + o(1)) \ln n\]

where $p_j$ is the reward density for this suboptimal machine.

Paper (regret bound, Auer 2022) shows the optimal logarithmic regret is also achievable uniformly over time.

Algorithm (UCB, upper confidence bound) At each round, chooses the arm with the highest upper confidence interval given by

\[\hat{X}_{j, t-1} + \sqrt{\frac{2\log(t)}{T_j(t-1)}}\]

The regret bound of this also grows logarithmically in $n$

Algorithm (Gradient Bandit Algorithm) choose the action based on preference $H$ instead of value function.

\[\pi_t(a) = \frac{\exp(H_t(a))}{\sum_b^k \exp(H_t(b))}\]

Preference is updated by

\[H_{t+1}(A_t) = H_t(A_t) + \alpha (R_t - \bar{R}_t) (1-\pi_t(A_t))\]

\[H_{t+1}(a) = H_t(a) - \alpha (R_t - \bar{R}_t)\pi_t(a)\]

depending on $a = A_t$ or $a \neq A_t$

It is a stochastic approximation to gradient ascent

1.2. Reinforcement Learning

The most important aspect in RL is that it uses training info that evaluates the action taken rather than instructs by giving correct action: it only indicates how good an taken action was, but do not tell whether it was the best or worst. In the instructive setting, the instruction is independent of the action taken.

A lot of machine learning problems are one-shot, in reinforcement learning, we care about sequential decisions: each decision we make have consequences in the future.

RL problems can be expressed as a system consisting an agent and an environment. The system repeats the following circles,

An environment produces information which describes the state $s_t$ of the system
An agent interacts with the environment by observing the state and using this information to select an action $a_t$.
The environment accepts the action and transitions into the next state, then return the next state and a reward $r_t$ to the agent

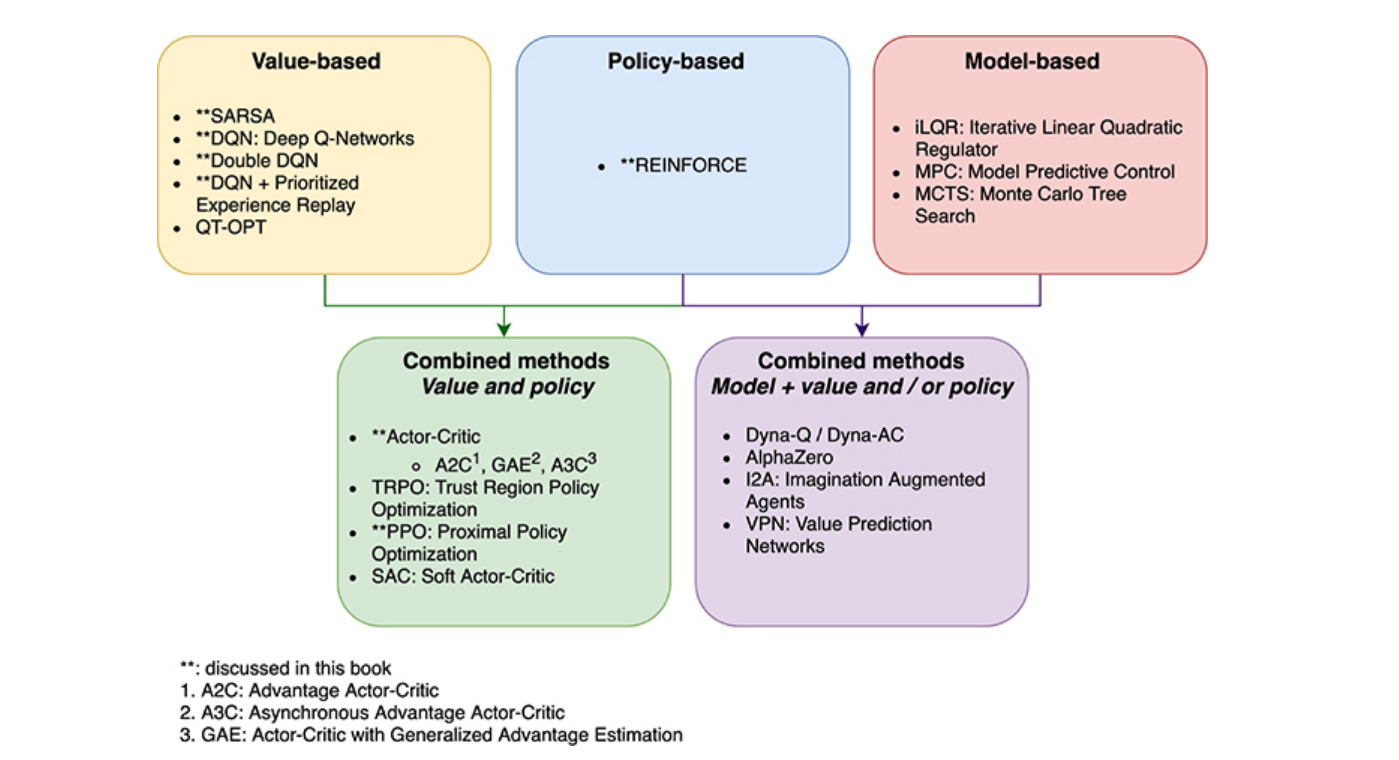
rl_family

A few concepts in RL are

Concept (prediction vs control):

prediction: evaluate the value function, also called evaluation problem
control: find the optimal policy

Concept (direct vs indirect RL)

direct RL: directly improve the value/policy from the real experience
indirect RL: learn the model first and then use it to do the planning

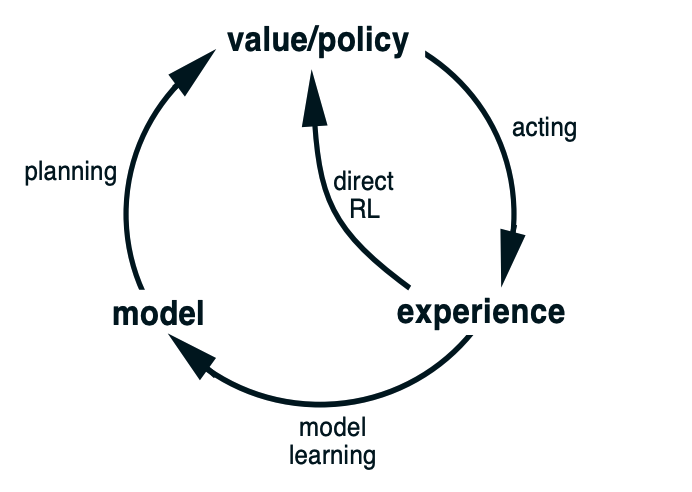
direct rl

Concept (model-based vs model-free) Whether an algorithm uses or estimates model's environment: transition probability distribution $P(s_{t+1}| s_t, a_t)$ and reward function.

By a model of the environment, we mean anything that an agent can use to predict how the environment will respond to its actions

distribution models: model produce a description of all possibilities and probabilities
sample model: a distribution model produce an individual possibility

Purely model based approaches are commonly applied to games with a target state: winning or lossing in a game. (e.g: MCTS (monte carlo tree search))

Advantage:

It allows the agent to plan by thinking ahead
sample efficiency

Disadvantage:

models are hard to come by
may learn irrelevant details

Concept (on-policy vs off-policy) Whether an algorithm learns with data gathered using just the current policy

1.2.1. MDP

MDPs is a classical formulation of sequential decision making, it extends bandit problems by introducing states where actions influence not just immediate rewards but also future states and rewards.

In bandit problems, we only estimate $q(a)$, in MDPs, we estimate $q(s,a)$ and $v(s)$.

We assume the the transition to the next state $s_{t+1}$ only depends on the previous state $s_{t}$ and action $a_t$, which is known as the markov property

\[s_{t+1} \sim P(s | s_{t}, a_t)\]

Definition (Markov Decision Process) Markov Decision Process is defined as a 4-tuple $(\mathcal{S}, \mathcal{A}, \mathcal{R}, P)$

$S$: state space (depend on previous state and action)
$A$: action space
$R$: reward space
$P$: transition prob summarizing MLP's dynamics: $p: \mathcal{S} \times \mathcal{R} \times \mathcal{S} \times \mathcal{A} \to [0, 1]$

\[p(s', r | s, a) := Pr(S_t = s', R_t = r, | S_{t-1}=s, A_{t-1}=a)\]

This four-arg dynamics function $p$ can be used to derive many other things:

For example, the transition prob distribution:

\[p(s' | s, a)= \sum_{r \in \mathcal{R}} p(s', r| s, a)\]

The expected reward

\[r(s, a) = \sum_r r \sum_{s'} p(s', r | s, a)\]

The interaction between environment and agent can be expressed in Python as

# Given an env (environment) and an agent

for episode in range(MAX_EPISODE):
    state = env.reset()
    agent.reset()

    for t in range(T):
        action = agent.act(state)
        state, reward = env.step(action)
        agent.update(action, state, reward)

        if env.done():
            break

The reward function is defined with respect to an episode $\tau = (s_0, a_0, r_0), ..., (s_T, a_T, r_T)$ the discount ratio $\gamma$

\[R(\tau) = r_0 + \gamma r_1 + \gamma^2 r_2 + ... = \sum_{t=1}^T \gamma^t r_t\]

The objective $J(\pi)$ is the expectations of the returns over many trajectories

\[J(\pi) = \mathbf{E}_{\tau \sim \pi}[R(\tau)]\]

A return $R_t$ of a trajectory is defined as the discounted sum of award from timestamp $t$ to the end of the trajectory

\[G_t = \sum_{t'=t}^T \gamma^{t'-t} R'_t\]

where both $G_t, R_t$ are random variables.

Definition (POMDP: partially observable MDP) is a generalization of MDP, which the agent cannot observe the underlying state. it only observes state partially through sensor, so there are two states:

observable state: the state observed by the agent
internal state: the state inside the environment

This is the actual model in the real-world

1.2.2. Policies and Value Functions

Definition (policy) A policy $\pi$ is how an agent produces the action in the environment to maximize the objective, it is a distribution over actions given state $\pi(a|x)$

Definition (state value Function) The state value function $v$ evaluates a state under a certain policy, it evaluates how good or bad a state is

\[v_{\pi}(s) = \mathbf{E}_{\tau \sim \pi}[G_t | S_t = s]\]

Definition (action value function, q) The action value function evaluates a (state, action) pair under a certain policy.

\[q_{\pi}(s, a) = \mathbf{E}_{\tau \sim \pi}[G_t | S_t = s, A_t = a]\]

Those functions can be estimated by taking average of randomly sample of actual returns (e.g: Monte Carlo) when there are few states. In the case there are very many states, it is practical to maintain $v_\pi, q_\pi$ as parametrized functions instead.

Definition (advantage function) advantage function is defined as

\[a_{\pi}(s, a) = q_{\pi}(s, a) - v_{\pi}(s)\]

Definition (Bellman Expectation Equation) Bellman Expectation Equation is defined with respect to a policy $\pi$

state value function can be derived from action value function

\[v_{\pi}(s) = \sum_{a}{\pi(a|s)q_{\pi}(s,a)}\]

action value function can be derived from next state value function

\[q_{\pi}(s,a) = \sum_{s', r} p(s', r | s,a) [r+\gamma v_\pi (s')]\]

Merging those two together, we get

\[v_\pi(s) = \sum_a \pi(a | s) \sum_{s', r} p(s', r | s, a) [r+\gamma v_\pi(s')]\]

1.2.3. Optimal Policies and Optimal Value Functions

Definition (Optimal Value Function) the optimal state value function is the maximum value function over all policies

\[v_{*}(s) = max_{\pi} v_{\pi}(s)\]

MDP is solved if we know the optimal action value function

\[q_{*}(s,a) = max_{\pi}(q_{\pi}(s,a))\]

It is well known that there exists an optimal policy $\pi^*$

Theorem (existence of Optimal Policy) a policy is better than another when its value function on all states should be better than the value function for the other. Note its proof is non-trivial since policy is partial order

Definition (Bellman Optimality Equation) optimal value function are recursively related by the Bellman optimality equations

\[v_{*}(s) = max_{a} q_{*}(s,a)\]

optimal action function can be expanded in the same manner

\[v_*(s) =\max_a \sum_{s', r} p(s', r | s, a) [r + \gamma v_*(s')]\]

Unfolding the action value function

\[q_{*}(s,a) = \sum_{s', r} p(s', r | s, a) [r + \gamma \max_{a'} q_*(s', a')]\]

Notice that Bellman expectation equation is taking sum, and Bellman optimality equation is taking max

Solution of Bellman Optimality Equation

nonlinear, no closed form solution in general
Iterative solution methods

2. Dynamic Programming (Model-based)

DP solves a fully known MDP by statically analyzing it (i.e. do not need to dynamically generating episodes)

Problem	Bellman Equation	Algorithm
Prediction	Bellman Expectation Equation	Iterative Policy Evaluation
Control	Bellman Expectation Equation + Greedy Policy Improvement	Policy Iteration
Control	Bellman Optimality Equation	Value Iteration

2.1. Policy Evaluation (Prediction)

Policy evaluation solves the following prediction problem:

Input: MDP, policy $\pi$
output: value function $v_\pi$

First we consider how to compute the state-value function $v_\pi$ for an arbitrary policy $\pi$.

If the dynamics $p$ (i.e. MDP) is completely known, then it can be iteratively solved using Bellman expectation backup

\[v_{k+1}(s) = \sum_a \pi(a|s) \sum_{s', r}p(s', r | s, a)[r+\gamma v_k(s')]\]

This algorithm is called iterative policy evaluation

More concretely, given a policy $\pi$, we iteratively update value function synchronously:

\[v_{0} \to \pi_1 \to v_{2} ... \to \v_pi\]

At each iteration, for all states $s \in S$
we update $v_{k+1}$ from $v_k(s')$ where $s'$ is a successor state of $s$

It can be shown the sequence $v_k$ converges to the fixed point $v_\pi$.

2.2. Policy Improvement

After policy iteration, we can improve the policy by acting greedily wrt $v_{\pi}$

\[\pi' = \text{greedy}(v_{\pi})\]

where $\pi' \geq \pi$

Theorem (policy improvement theorem) Let $\pi, \pi'$ be any deterministic policies such that if for all $s$

\[q_\pi(s, \pi'(s)) \geq v_\pi(s)\]

then the policy $\pi'$ must be as good as, or better than $\pi$:

\[v_{\pi'} (s) \geq v_\pi(s)\]

Using this theorem, we can suggest the following policy improvement algorithm

Model (policy improvment) Given a policy $\pi$, Evaluate the policy to get $v_{\pi}(s)$ Improve the policy to $\pi'$ by acting greedily with respect to $v_{\pi}$

\[\begin{aligned}\pi'(s) &= \text{argmax}_a q_\pi \\ &= \text{argmax}_a \sum_{s', r} p(s',r | s, a)[r + \gamma v_\pi(s')]\end{aligned}\]

2.3. Policy Iteration (Control)

Policy Iteration solves the following control problem:

Input: MDP
output: optimal value function $v_*$ and optimal policy $\pi_*$

policy_iteration

Model (policy iteraion) By repeating policy evaluation and policy improvment, we get the policy iteration algorithm.

\[\pi_0 \to v_{0} \to \pi_1 \to v_{\pi_1} ... \to \pi_\star \to v_\star\]

No matter how we choose $\pi_0 and $v_{0}$, this policy iteration always converges to $\pi_{*}$: when the new greedy policy has the same value function as the old policy

\[v_{\pi'(s)} = \max_a \sum_{s', r} p(s', r | s, a)[r + \gamma v_{\pi'}(s')]\]

This satisfies the Bellman optimality equation, which indicates $v_\star = v_{\pi'}$

A simple proof of convergence can be found in David Silver's lecture slide

One drawback of policy iteration is the policy evaluation is expensive to converge. In general, we do not need to wait until the value function converge.

Model (generalized policy iteration) we let the policy-evaluation and policy-improvment processes interact, independent of the granularity and other details of the two processes.

Value Iteration (control)

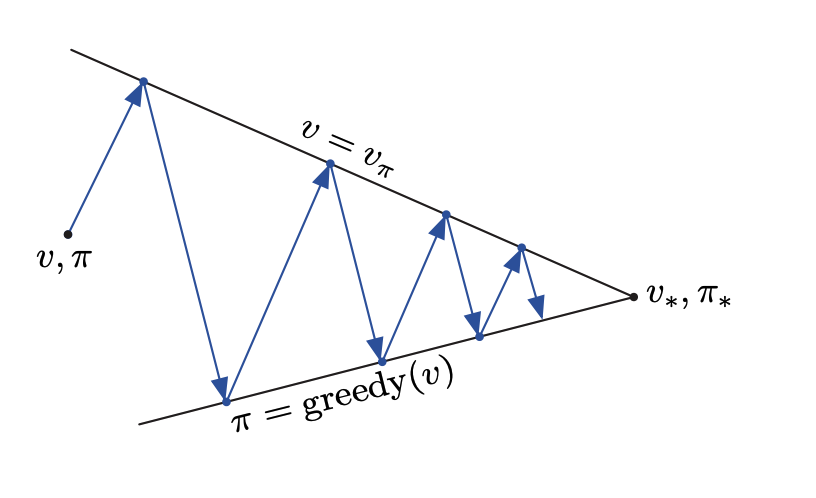
value iteration can be seen as an instance of generalized policy iteration where we we update policy every time updating the value function (i.e. only doing one sweep of policy evaluation).

Policy improvement and truncated policy evaluation can be combined into the following Bellman optimality backup:

\[v_{k+1}(s) = \max_a \mathbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) | S_t = s, A_t = a]\]

For arbitrary $v_0$, the sequence $\{ v_k \}$ converges to $v_*$

Intuitively, value iteration start with final rewards and work backwards.

Note the difference between value iteration and policy evaluation is this one is taking max instead of sum.

2.4. Asynchronous Dynamic Programming

DP above are synchronous backups where all states are updated in a 'lockstep' (i.e. expensive)

Asynchronous DP updates states individually in any order. It is guaranteed to converge if all states continue to be selected.

Three simple ideas for async DP:

in-place DP: update state in-place (i.e. only stores one copy of value function)
prioritised sweeping: use a priority queue to keep track of most likely affected states after each update
realtime DP: use agent experience (episode) to select states to be updated

3. Monte Carlo Methods

MC method can work with both model-based and model-free settings

Unlike the DP, in MC method, we do not need to assume complete knowledge of the environment: we only require experience (i.e. sample complete episode from the actual experience.)

3.1. On-policy Prediction

MC methods learn from the full episode

In DP, we computed value functions from knowledge of MDP, here we learned value functions from sample returns using empirical mean return

Model (MC prediction) updates of value function happen after end of every episode and complete return

\[V(s) = V(s) + \frac{1}{N(s)}(G_t - V(s))\]

There are two flavors:

in first-visit MC, update is happening when state $s$ is visited for the first time $t$ in an episode, $N(s)$ is the total number of episodes when state $s$ is ever visited so far
in every-visit MC, update is happening evertime state $s$ is visited at timestamp $t$ where $N(s)$ is the total number of appearances in all episodes so far

By law of large numbers, when $N(s) \to \infty$,

\[V(s) \to v_{\pi}(s)\]

Note that if a model is available, we still use the state value functions $v_\pi(s)$

When the model is not available, so we typically estimate action value function $Q_\pi(s,a)$ instead of $V_\pi(s)$

We sample a full episode using $\pi$: $\{ S_1, A_1, R_1, S_2, ... \} \sim \pi$. For each state $S_t$ and action $A_t$ in an episode, we update $Q_\pi(s, a)$ as following

\[N(S_t, A_t) = N(S_t, A_t) + 1\]

\[Q(S_t, A_t) = Q(S_t, A_t) + \frac{1}{N(S_t, A_t)}(G_t - Q(S_t, A_t))\]

3.2. On-policy Control

In the model-free settings, we cannot do policy improvement using state value function $V_\pi(s)$ since we do not know MDP dynamics.

Instead of using $V_\pi(s)$, we use action value function $Q_\pi(s, a)$ where policy improvment is done using:

\[\pi(s) = \text{argmax}_a q(s,a)\]

We can do similar pilicy iteration in the following manner:

\[\pi_0 \to q_{\pi_0} \to \pi_1 ... \to \pi_\star \to q_\star\]

Greedy policy improvement in this case cannot explore all states and actions and fails to be optimized.

To guarantee the convergence, it requires the assumption of the exploring starts

mc convergence

To be efficient, we do not need to wait until $Q_\pi$'s convergence. We can update policy after every episode

mc convergence

3.3. Off-policy Prediction

Off-policy methods are of greater variance and are slower to converge, but they are more powerful and general. It allows the agent to learn from a more diverse set of experiences, which can help it to explore the environment more effectively

There are two policies involved:

target policy: policy being learned
behaviror policy: the policy used to generate behavior

We want to estimate $v_\pi$ or $q_\pi$ (target policy) but episodes are following another policy $b$ (behavior policy).

There is a constraint called coverage which says $\pi(a|s) > 0$ must imply $b(a | s) > 0$

Almost all off-policy methods are using importance sampling (my note)

Given a episode $A_t, S_{t+1}, A_{t+1}, ..., S_T$ and its return $G_t$, first, notice that the expectation gives value function of the behavior policy, not the target policy:

\[v_b(s) = E[G_t | S_t = s]\]

To apply importance sampling, we need to consider the relative probability ratio under two difference policies

Given a episode $A_t, S_{t+1}, A_{t+1}, ..., S_T$

\[\rho_{t:T-1} = \frac{P(A_t, ..., S_T | \pi)}{P(A_t, ..., S_T | b)} = \frac{\prod \pi(A_k | S_k) p(S_{k+1} | S_k, A_k)}{\prod b(A_k | S_k) p(S_{k+1} | S_k, A_k)} = \prod \frac{\pi(A_k | S_k)}{b(A_k | S_k)}\]

Using this ratio, we obtain the value function of target policy

\[v_\pi(s) = E[\rho_{t:T-1} G_t | S_t = s]\]

To estimate $v_\pi(s)$ using previous formula, we can do the ordinary importance sampling

\[V(s) = \frac{\sum_{t \in \tau(s)} \rho_{t:T(t)-1} G_t}{|\tau(s)|}\]

where $\tau(s)$ is the set of all timestamps in which state $s$ is visited

or the weighted importance sampling

\[V(s) = \frac{\sum_{t \in \tau(s)} \rho_{t:T(t)-1} G_t}{\sum_{t \in \tau(s)} \rho_{t:T(t)-1}}\]

In the first-visit methods, ordinary importance sampling is unbiased with large variance, weighted importance sampling is biased (asymptotically unbiased) but with much smaller variance and is strongly preferred. In the every-visit method, both are biased.

3.4. Off-policy Control

why we want off-policy:

learn from human and other agents
re-use experience from old policies: $\pi_0, \pi_1, ..., \pi_{t-1}$
learn about optimal policy while following exploratary policy
learn from multiple policies while following one policy

4. Temporal-Difference Learning

TD learning is also model-free methods, which do not require knowledge of MDP transitions/rewards. Note it works for model-based method as well.

Instead of using complete episode, TD learning is using incomplete episodes (or partial episodes), by bootstraping

TD vs MC

MC has high variance, zero bias

good convergence properties (even with function approximation)
not sensitive to initial value

TD has low variance, some bias

usually more efficient than MC
TD(0) converges to $v_\pi(s)$ but not always with function approximation
more sensitive to initial value
usually limited to discrete actions

TD vs DP

TD can be seen as the sampling version of DP as the following figure shows:

td_vs_dp

4.1. TD Prediction

Recall Monte Carlo do the following prediction

\[V(S_t) = V(S_t) + \alpha (G_t - V(S_t))\]

where $G_t$ is the actual return following time $t$. It means we must wait until the end of the episode to determine the increment to $V(S_t)$

In contrast, TD methods use cached value instead of the waiting complete actual return. For example,

Model (TD(0)) it updates value $V(S_t)$ toward estimated return $R_{t+1} + \gamma V(S_{t+1})$ instead of the actual return $G_t$

\[V(S_t) = V(S_t) + \alpha(R_{t+1}+\gamma V(S_{t+1})-V(S_t))\]

where $R_{t+1}+\gamma V(S_{t+1})$ is called TD target and $R_{t+1}+\gamma V(S_{t+1})-V(S_t)$ is referred to as TD error

Because it bases its update in part on an existing estimate, it is called bootstrapping method.

The comparison between MC (left) and TD (right) can be illustrated as following

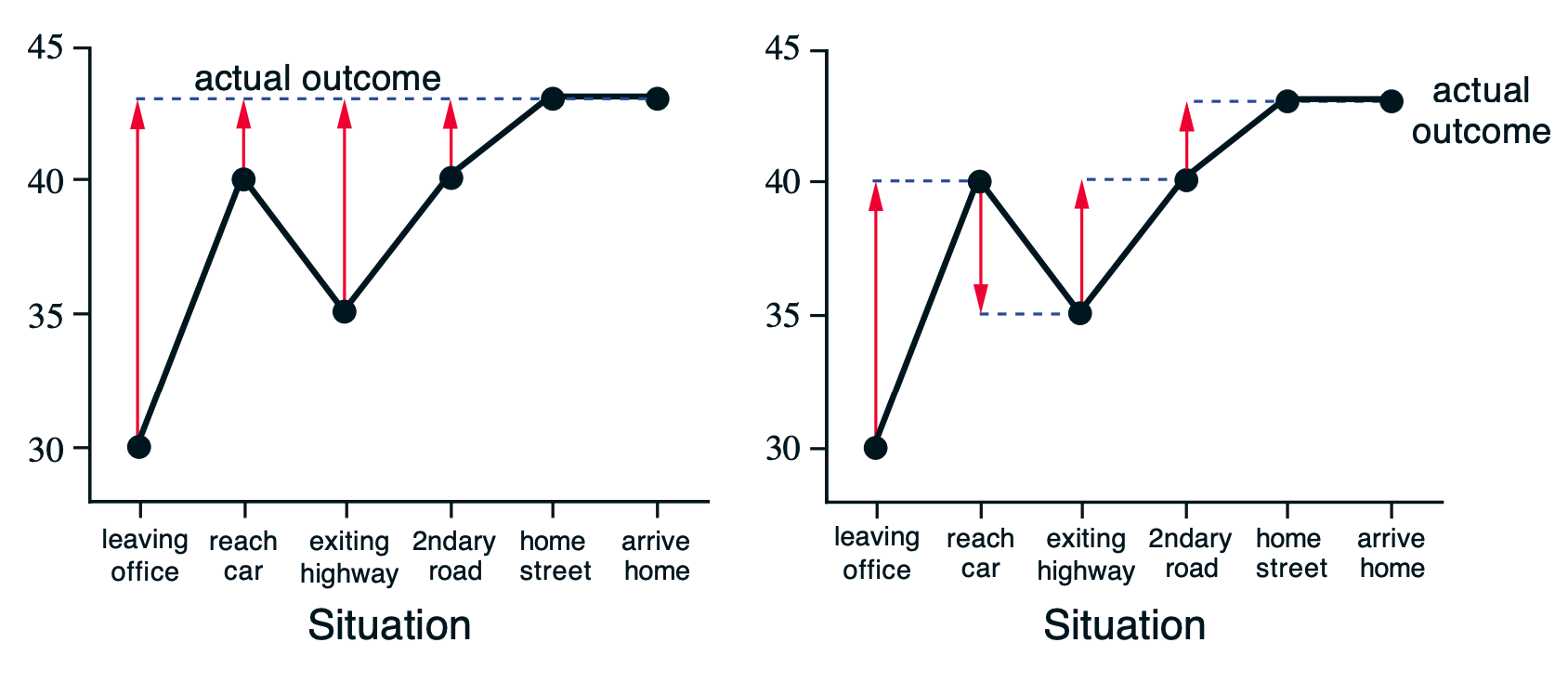comparison (Reference: from RL Book 2^nd version)

There is a bias/variance tradeoff

return $G_t$ is an unbiased estimate of $v_\pi(S_t)$, the true TD target is also unbiased $R_{t+1} + \gamma v_\pi(S_{t+1})$
The actual TD target $R_{t+1} + \gamma V(S_{t+1})$ is biased
however, TD target has much lower variance
this is because return $G_t=R_{t+1}+\gamma R_{t+2}+..$ depends on many random variable $R_t$, but TD target has only one random variable

It can be generalize to look n steps into the future

Model (n-step TD prediction): TD can be extended into n-step methods

$n=1$ (TD): $G_t^{(1)} = R_{t+1} + \gamma V(S_{t+1})$
$n=2$: $G_t^{(2)} = R_{t+1} + \gamma V(S_{t+2}) + \gamma^2 V(S_{t+2})$
$n=\infty$: (MC) $G_t^{(\infty)} = R_{t+1} + \gamma V(S_{t+2}) + \gamma^2 R_{t+3} + ...$

where the n-step return

\[G_{t}^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n})\]

and n-step TD prediction is

\[V(S_t) = V(S_t) + \alpha (G_t^{(n)} - V(S_t))\]

we can average multiple n steps

Model (TD($\lambda$) prediction) TD(lambda) combines all n-steps return with decaying weight.

\[G_t^{\lambda} = (1-\lambda)\sum {\lambda^{n-1} G^{(n)}_t}\]

4.2. On-policy TD Control (SARSA)

Instead of using TD to update state values, we use TD to update action values with a tuple $(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})$

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha [ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]\]

See the following algorithm:

sarsa

SARSA converges to the optimal action-value function under some regularities

\[Q(s, a) \to q_*(s, a)\]

Model (n-step SARSA) SARSA can be extended to n-step as well where

$n=1$ (SARSA): $q_t^{(1)} = R_{t+1} + \gamma Q(S_{t+1})$
$n=2$: $q_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 Q(S_{t+2})$
$n=\infty$ (MC): $q_t^{(\infty)}=R_{t+1} + \gamma R_{t+2} + ...$

The n-step SARSA updates $Q(s,a)$ towards the n-step Q-return

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha (q_t^{(n)} - Q(S_t, A_t))\]

Model (SARSA($\lambda$)) we also have the Sarsa($\lambda$), which combines all n-step $q_t^{(n)}$ as well

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha (q_t^{\lambda} - Q(S_t, A_t))\]

where

\[q_t^{\lambda} = (1-\lambda)\sum_n \lambda^{n-1} q_t^{(n)}\]

4.3. Off-policy TD Control (Q-Learning)

The most general Q-learning has the following form

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha [ R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t, A_t)]\]

while $A'$ is sampled from the behavior policy $A' \sim b(a | S_{t+1})$ instead of the target policy $A_{t+1} \sim \pi(a | S_{t+1})$

Model (Q-learning) The most commonly used Q-learning (Watkins, 1989)³ was one of the early breakthroughs in RL

It learned the action value function $Q$ to directly approximate the optimal action-value function $q_*$, independent of the policy being followed:

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha [ R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]\]

The following term is called Bellman error, which we want to minimize. It becomes 0 in Bellman optimality equation

\[R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)\]

Under some regularities, it is shown that $Q$ converges with probability 1 to $q^*$

Q-learning is an off-policy as the next action $a$ is obtained by maximizing $Q$ instead of following current policy $\pi$. This characteristic also allows us to do $\epsilon$-greedy policy to explore (since it is off-policy)

algo

Model (expected SARSA) Another variant is to take expectation for backup

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha [ R_{t+1} + \gamma \mathbb{E}_{\pi} [Q(S_{t+1}, A_{t+1} |S_{t+1}] - Q(S_t, A_t)]\]

It is more computational expensive, but eliminates the variance due to the random selection of $A_{t+1}$

Expected Sarsa can be used on-policy, but in general, the policy $\pi$ can be different from the target policy to generate behavior, in which case it becomes an off-policy.

Richard S Sutton and Andrew G Barto. 2018. Reinforcement learning: An introduction. MIT press. ↩
David Silver. 2015. Lectures on reinforcement learning. ↩
Christopher John Cornish Hellaby Watkins. 1989. Learning from delayed rewards. ↩