0x001 Topology
- 1. Topological Space
- 2. Continuous Function
- 3. Topological Properties
- 4. Countability and Separation Axioms
- 5. Baire Space
- 6. Metric Space
- 7. Fundamental Group
- 8. Reference
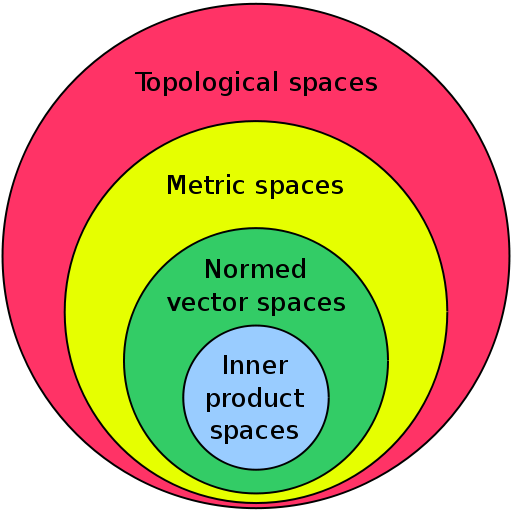
This note mainly deals with topological space and metric space, normed space and inner product spaces will go to the algebra and analysis pages.
1. Topological Space
Definition (topology) Let \(X\) be a non-empty set. A set \(\mathcal{T}\) of subsets of \(X\) is said to be topology on \(X\) iff
- \(X \in \mathcal{T}, \emptyset \in \mathcal{T}\)
- union of any number of sets of \(\mathcal{T}\) belongs to \(\mathcal{T}\)
- interaction of any two sets of \(\mathcal{T}\) belongs to \(\mathcal{T}\)
The pair \((X, \mathcal{T})\) are called topological space
discrete, indiscrete topology
There are two trivial topological space for any \(X\), \(2^X\) is the discrete topology of \(X\), \(\{ \emptyset, X \}\) is the indiscrete topology of \(X\).
finite complement topology (cofinite topology)
Let \(X\) be a set, \(\mathcal{T}\) be the collection of all subsets \(U \subset X\) such that \(X - U\) is either finite or all of \(X\)
Definition (finer, coarser) Suppose \(\mathcal{T}, \mathcal{T'}\) are two different topologies on a given set \(X\), if \(\mathcal{T} \subset \mathcal{T'}\), then \(\mathcal{T}\) is a coarser and \(\mathcal{T'}\) is a finer topology
1.1. Basis
Defining the entire set of \(\mathcal{T}\) is too difficult, we can instead specify a smaller collection of subset of \(X\) and define topology on top of that. This is called basis.
Definition (basis) If \(X\) is a set, a basis of a topology on \(X\) is a collection \(\mathcal{B}\) of subsets such that
- for \(x \in X\), there exists a \(B \in \mathcal{B}\) containing it
- if \(x \in B_1 \cap B_2\), then there exists a \(B_3 \subset B_1 \cap B_2\) that contains \(x\)
If \(\mathcal{B}\) satisfies these conditions, it defines a topology.
example of basis
Examples of basis
- the collection of one-point set of \(X\) is the basis of the discrete topology of \(X\)
- In a metric space, the collection of all open balls forms a base for the topology
basis example of R
The standard topology is the topology generated by the collection of all open intervals
The lower limit topology is generated by the half-open intervals
The K-topology is generated by the collection of all open intervals \((a,b)\) along with all sets of the form \((a,b)-K\) where \(K = \{ 1/n | n \in \mathbb{Z}_{+} \}\)
Basis and open sets are two characterizations of topology, they can be used to build each other.
Lemma (open sets defined by basis) A subset \(U\) of \(X\) is called open if for every \(x \in U\), there exists a basis element \(B\) such that \(x \in B\) and \(B \subset U\)
This indicates that each open set \(U\) can be expressed as a union of basis elements.
We can also use topology to generate/decide a basis
Lemma (basis defined by a open sets) Let \(X\) be a topological space. Suppose \(\mathcal{C}\) is a collection of open set such that for each open set \(U\) in \(X\) and every point \(x \in U\), there exists an element \(C \in \mathcal{C}\) such that \(x \in C \subset U\). Then \(\mathcal{C}\) is a basis for the topology of \(X\)
Basis can be used to decide whether one topology is finer than another, for example
Lemma (finer criterion) Let \(\mathcal{B}, \mathcal{B}'\) be bases of topology \(\mathcal{T}, \mathcal{T}'\), then \(\mathcal{T}'\) is finer than \(\mathcal{T}\) iff for each \(x \in X\) and each basis \(B \in \mathcal{B}\) containing \(x\), there is a basis \(B' \in \mathcal{B}'\) such that \(x \in B' \subset B\)
Definition (subbasis) A collection of subsets \(\mathcal{S}\) is called subbasis of \(X\) if its union equals \(X\).
The topology generated by \(\mathcal{S}\) is defined to be the collection of all unions of all finite intersection of \(\mathcal{S}\)
Subbasis \(\mathcal{S}\) first creates a basis \(\mathcal{B}\) by taking the finite intersection, then the basis generates the topology by taking union
1.2. Open set and Closed set
Definition (open set) \(U \subset X\) is an open set iff \(U \in \mathcal{T}\)
Definition (neighborhood) \(U\) is a neighborhood of \(x\) if \(U\) is a open set containing \(x\)
Note there are some book defining neighborhood to be a subset contains an open set containing \(x\), which indicate neighborhood does not need to be open. In this note, we assume neighborhood is always open.
Definition (closed) A subset of \(A\) of a topological space \(X\) is closed if the set \(X - A\) is open
Definition (interior, closure)
- the interior of \(A\) is defined as the union of all open sets contained in \(A\)
- the closure of \(A\) is defined to be the intersection of all closed sets containing \(A\)
Lemma (closure) if \(x \in \bar{A}\) then every neighborhood of \(x\) intersect \(A\)
Lemma (closure in subspace) Let \(Y\) be a subspace of \(X\), \(A\) be a subset of \(Y\). let \(\bar{A}\) be the closure of \(A\) in \(X\). Then the closure of \(A\) in \(Y\) is \(\bar{A} \cap Y\)
limit point is another way to describe closure
Definition (limit point, accumulation point) We say \(x\) is a limit point of \(A\) if every neighborhood of \(x\) intersect \(A\) in some point other than \(x\) itself.
let \(A'\) be the set of all limit points of \(A\), then closure is characterized as
limit points
Let \(A=(0, 1]\), then \([0, 1]\) are all limit points
Let \(B=\{ 1/n | n \in \mathbb{Z}_+ \}\), then limit point of \(B\) is only 0
Definition (convergence) A sequence \(x_1, ...\) of points in \(X\) converges to \(x\) if for each neighborhood \(U\) of \(x\), there exists an \(N\) such that all \(n \geq N\), \(x_n \in U\).
convergence to two points
Consider the topology \(\{ \emptyset, \{a, b\}, \{b, c\}, \{b\}, \{a,b,c \} \}\) on \(\{a, b, c \}\). The sequence \(b, b, b...\) converges to \(a,b,c\)
Definition (Fréchet, T1) For every pair of distinct point, each has a neighborhood that does not contain the other
Lemma (singleton is closed) It is easy to see that each single point (singleton) in T1 space is closed, therefore finite point sets are closed.
The Hausdorff condition is generally considered to be a very mild extra condition to impose on a topological space.
Definition (Hausdorff, T2) A topological space \(X\) is called a Hausdorff space if for every distinct point \(x_1, x_2\), there exists disjoint open neighborhoods \(U_1, U_2\) such that \(x_1 \in U_1, y_1 \in U_2\)
Theorem (unique convergence) If \(X\) is Hausdorff, then a sequence of points on \(X\) converges to at most one point of \(X\)
1.3. Construction
1.3.1. Order Topology
Definition (order topology) Let \(X\) be a set with simple order relation. Assume \(X\) has more than one element, then the following collection \(\mathcal{B}\) is a basis for a topology on \(X\), called order topology
- All open set \((a,b)\)
- All interval \([-\infty, b)\) if the smallest \(-\infty\) exists
- All interval \((a, \infty]\) if the largest \(\infty\) exists
1.3.2. Subspace Topology
Definition (subspace) Let \(X\) be a topological space with topology \(\mathcal{T}\). If \(Y\) is a subset of \(X\), the collection
is a topology on \(Y\), called the subspace topology
1.3.3. Product Topology
Definition (box topology) Let \(\{ X_\alpha \}_{\alpha \in J}\) be an indexed family of topological spaces, the collection of all sets of the form
forms a basis for the product space \(\prod_{\alpha \in J} X_{\alpha}\), and this topology is called the box topology
Definition (product topology) Consider the collection
The topology generated by the subbasis \(S\) is called the product topology.
1.3.4. Quotient Topology
Definition (quotient map) Let \(X,Y\) be topological spaces, let \(p X \to Y\) be a surjective map, the map is said to be a quotient map if a subset \(U\) is open in \(Y\) iff \(p^{-1}(U)\) is open in \(X\).
Definition (quotient topology) If \(X\) is a space and \(A\) is a set and if \(p: X \to A\) is a surjective map, then there exists exactly one topology \(\Tau\) on \(A\) relative to which \(p\) is a quotient map. The topology is defined such that \(U\) is open if \(p^{-1}(U)\) is open.
Definition (quotient space) Let \(X\) be a topological sapce, \(X^*\) be a partition of \(X\) into disjoint subsets whose union is \(X\). Let \(p: X \to X^*\) be a surjective map that carries each point of \(X\) to the elements of \(X^*\) containing it. In the quotient topology induced by \(p\), the space \(X^*\) is called a quotient space of \(X\).
2. Continuous Function
Continuity is an definition not only depending on function itself, but also on topologies of \(X,Y\)
Definition (continuity) Let \(X,Y\) be a topological spaces, a function \(f: X \to Y\) is said to be continuous if for each open subset \(V\) of \(Y\), the inverse image \(f^{-1}(V)\) is an open set of \(X\)
Criterion (continuity) To prove continuity of \(f\), it is sufficient to check the inverse of basis or subbasis element:
- the inverse of every basis element of \(f\) is open
- the inverse of every subbasis element is open
Criterion (continuity) The followings are equivalent
- \(f\) is continuous
- for every subset \(A\), \(f(\bar{A}) \subset \overline{f(A)}\)
- For every closed subset \(B \subset Y\), the set \(f^{-1}(B)\) is also closed in \(X\)
- For each \(x \in X\) and each neighborhood \(V\) of \(f(x)\), there is a neighborhood \(U\) of \(x\) such that \(f(U) \subset V\)
2.1. Sequential Continuity
Definition (sequential continuity) for every sequence \(x_n \to x\) , the sequence \(f(x_n) \to f(x)\)
continuity implies sequential continuity, but not vice versa in general. Those two concepts are equivalent for example, in metric space and second-countable spaces
2.2. Homeomorphism
Homeomorphism is a bijective correspondence that preserves topological properties (properties defined using open sets). It is analogous to isomorphism which preserves algebraic structure. (e.g. linear isomorphism preserves linear properties between vector spaces by associaciating with a invertible matrices)
Definition (homeomorphism) Let \(X,Y\) be topological spaces, let \(f: X \to Y\) be bijection. If both \(f\) and its inverse are continuous, then \(f\) is called homeomorphism
Another way to say homeomorphism is that \(f\) is a bijective such that \(f(U)\) is open iff \(U\) is open.
One popular example of homeomorphism is the Poincaré conjecture
statement of Poincaré conjecture
Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.
Definition (topological imbedding) Suppose \(f: X \to Y\) is an injective continuous mapping, let \(Z\) be the image set of \(f(X)\) and suppose the restriction \(f': X \to Z\) is a homeomorphism then we say the map \(f: X \to Y\) is a topological imbedding of \(X\) \in \(Y\)
2.3. Construction
Theorem (construction of continuous functions) Let \(X,Y,Z\) be topological spaces
- (constant function) If \(f: X \to Y\) maps all of \(X\) into the single point \(y_0\) of \(Y\). Then \(f\) is continuous
- (inclusion) If \(A\) is a subspace of \(X\), the inclusion function \(j: A \to X\) is continuous
- (composite) If \(f: X \to Y, g: Y \to Z\) are continous, then \(g \circ f: X \to Z\) is continuous
- (domain restriction) If \(f: X \to Y\) is continuous, if \(A\) is a subspace of \(X\), then restricted functio n\(f|A: A \to Y\) is continuous
- (range restriction or expansion) Let \(f: X \to Y\) be continuous, If \(Z\) is a subspace of \(Y\) containing the image set \(f(X)\) or \(Z\) is a space containing \(Y\) as subspace, the function \(f: X \to Z\) is continuous
- (local formulation of continuity) The map \(f: X \to Y\) is continuous if \(X\) can be written as a union of \(U_{\alpha}\) such that \(f|_{U_{\alpha}}\) is continuous for every \(\alpha\)
The following pasting lemma can be used to construct continuous function from pieces of functions.
Lemma (pasting lemma) Let \(X = A \cup B\) where \(A,B\) are closed in \(X\). Let \(f: A \to Y, g: B \to Y\) be continuous and if \(f(x)=g(x)\) for all \(x \in A \cap B\), then the combined function is continuous: \(h: X \to Y\) with \(h(x) = f(x)\) if \(x \in A\) and \(h(x) = g(x)\) if \(x \in B\)
Theorem (maps into products) Let \(A \to X \times Y\) be the given equation
Then \(f\) is continuous iff the function
are continuous
3. Topological Properties
3.1. Connectedness
The concept of connectedness is useful to prove the intermediate value theorem. It is a topological property as it is formulated entirely in terms of collection of open sets
Definition (connected space) Let \(X\) be a topological space, A separation of \(X\) is a pair \(U,V\) of disjoint open subsets of \(X\) whose union is \(X\). The space is said to be connected if there is no separation of \(X\).
Another way to state connectedness: A space \(X\) is connected iff the only subsets of \(X\) that are both open and closed are the empty set and \(X\) itself
Definition (connected subspace) If \(Y\) is a subspace of \(X\), a separation of \(Y\) if a pair of disjoint sets \(A,B\) where \(Y=A \cap B\), and \(\bar{A} \cap B\) and \(A \cap \bar{B}\) are both empty. The space \(Y\) is connected if there exists no separation of \(Y\)
Roughly \(\bar{A} \cap B \neq \emptyset\) means \(A\) has a limit point in \(B\) therefore \(A\) is not closed and \(B\) is not open.
rational is not connected
\(Q\) is not connected. We can write Q as \(A \cup B\) where
where \(\hat{A} \cap B = A \cap \hat{B} = \emptyset\)
Lemma A set \(E \subset R\) is connected iff whenever \(a < c < b\) with \(a,b\in E\) it follows that \(c \in E\)
The following theorem generalizes the intermediate value theorem
Theorem (continuity preserves connectedness) The image of a connected subspace under a continuous map is connected.
3.2. Compactness
compactness is a concept generalizing a bounded closed set. From the beginning of topology, it was clear that closed interval had a certain property that is crucial for theorems such as maximum value theorem and uniform continuity theorem.
However, it was not clear how to generalize for arbitrary topological space. One effort was defining "limit point" compactness using limit points
This definition was originally called "compactness" but was later realized not the essential definition. The latter formulation is what we now call compactness using open covers.
Definition (open cover) Suppose \(A \subset R\), a collection \(\mathcal{C}\) of open subsets of \(R\) is called an open cover of \(A\) if \(A\) is contained in the union of all the sets in \(\mathcal{C}\)
Definition (finite subcover) An open cover \(\mathcal{C}\) of \(A\) is said to have a finite subcover if \(A\) is contained in the union of some finite list of sets in \(\mathcal{C}\)
Definition (compactness) A set \(K \subset R\) is compact if every open cover for \(K\) has a finite subcover
For example, if the set \(K\) only contains finite elements, then obviously it is compact.
real line is not compact
The real line \(R\) is not compact. Consider a cover of
It does not have any finite subcover
compact example
The following set is compact
For any open cover of \(A\), we can pick an open set \(U\) containing \(A\), this set \(U\) should contain infinitely many tails \(1/n\), the remaining elements are finite, so it is easy to pick up their cover.
characterization of compactness in R, Heine-Borel
Following statements are equivalent in \(\mathbb{R}\)
- \(K\) is sequential compact
- \(K\) is closed and bounded
- \(K\) is compact
Proof
-
\(1 \to 2\): Suppose \(K\) is not bounded, then we can pick up a sequence \((x)_n\) such that \(x_n \geq n\), which suggests any subsequence \(x_{n_k} \geq n_k\) is also not bounded. However, compactness can select a convergent subsequence, and this subsequence must be bounded. therefore, we have a contradiction. Next, consider any limit point \(x\) for \(K\), there must be a sequence \((x)_n \in K\) converging to \(x\), then any subsuquence must converge to \(x\) including the sequence picked up by compactness, the compactness says the convergent point must be in \(K\) so we know \(x \in K\), so all limit point is contained and \(K\) is closed
-
\(3 \to 2\): To show the boundedness, construct a cover consisting of open balls with radius 1 at every \(x \in K\), then compactness gives a finite subcover, then take the max and min. To show the closedness, suppose it is not closed: there exists a limit point \(y \notin K\) and \(y_n \in K \to y\). For every point \(x \in K\), construct a open ball with radius \(|x-y|/2\), compactness again gives a finite subcover where we can take the max, the max however is strictly less than \(y\), therefore the finite subcover cannot cover tails of \(y_n\)
-
\(2 \to 3\): This is actually the Heine Borel Theorem. The basic idea is to first show \([a,b]\) is compact by consider the sup of finite covered element, and use this fact to show a random closed bounded set is compact.
3.3. Limit Point Compactness
Limit point compactness is weaker than compactness in general, but equivalent with compactness for metrizable spaces
Definition (limit point compactness, weakly countable compactness) A space \(X\) is said to be limit point compact if every infinite subset of \(X\) has a limit point
Definition (sequentially compact) Let \(X\) be a topological space and \(x_n\) be a sequence of \(X\). The space \(X\) is said to be sequentially compact if every sequence of \(X\) has a convergence subsequence
Theorem (compactness equivalence over metrizable space) Let \(X\) be a metrizable space. Then the following are equivalent:
- compact
- limit point compact
- sequential compact
3.4. Local Compactness
Definition (local compactness) A space \(X\) is said to be locally compactness at \(x\) if there is some compact subspace \(C\) of \(X\) contains a neighborhood of \(x\).
If \(X\) is locally compact at every point \(x\), then \(X\) is said to be local compact.
4. Countability and Separation Axioms
4.1. Countability Axioms
Definition (first countable) A space \(X\) is said to have a countable basis at \(x\) if there is a countable collection \(\mathcal{B}\) of neighborhoods of \(x\) such that each neighborhood of \(x\) contains at least one of the element of \(\mathcal{B}\).
A space that has a countable basis at each of its points is said to satisfy the first countability axiom, or to be first-countable.
5. Baire Space
Definition (Baire space) A space is said to be a Baire space if given any countable collection \(\{ A_n \}\) of closed sets of \(X\) each of which has empty interior in \(X\), their union \(\cup A_n\) also has empty interior in \(X\).
Definition (Baire category theorem) If \(X\) is a compact Hausdorff space or a complete metric space, then \(X\) is a Baire space
6. Metric Space
6.1. Metric Topology
Definition (metric) A metric on a set \(X\) is a function:
having the following properties:
- \(d(x,y) \geq 0\)
- \(d(x,y) = d(y,x)\)
- \(d(x,y) + d(y,z) \geq d(x,z)\)
Definition (metric topology) If \(d\) is a metric on \(X\), the collection of all \(\epsilon\)-balls \(B_d(x, \epsilon)\) for \(x \in X, \epsilon > 0\) is a basis for a topology of \(X\), called the metric topology induced by \(d\)
Definition (metrizable space) If \(X\) is a topological space, \(X\) is said to be metrizable if there exists a metric \(d\) on the set \(X\) that induces the topology of \(X\)
Metrizability is always a desirable property for a space, therefore a important problem is to find conditions on a topological space that will guarantee it is metrizable. For example, Urysohn’s metrization theorem.
6.2. Metrization
An important problem in topology is to find conditions on a topological space that guarantee it is metrizable, it is expressed, for example, in the Urysohn metrization theorem
7. Fundamental Group
One of the basic problem of topology is to determine whether two given topological space are homeomorphic or not.
7.1. Homotopy of Paths
Definition (homotopy) If \(f, f'\) are continuous map of spaces \(X \to Y\). We say \(f\) is homotopic to \(f'\) if there is a continuous map \(F: X \times I \to Y\) such that for each \(x\)
The map \(F\) is called a homotopy between \(f\) and \(f'\). If \(f\) is homotopic to \(f'\), we write \(f \simeq f'\)
8. Reference
[1] Topology 2nd Edition Munkres
[2] Abbott, Stephen. Understanding analysis. Vol. 2. New York: Springer, 2001.
[3] Tao, Terrence. "Analysis (Volume 1)." Hindustan Book Agency (2006).