0x221 Microarchitecture

• 1. Arithmetic
  • 1.1. Integer
  • 1.2. Real Numbers
    • 1.2.1. Fixed-point Representation
    • 1.2.2. Float Representation
      • 1.2.2.1. Rounding
• 2. Processor
  • 2.1. Notable CPU
  • 2.2. Flynn's taxonomy
    • 2.2.1. SISD
    • 2.2.2. SIMD
    • 2.2.3. MISD
    • 2.2.4. MIMD
  • 2.3. Pipeline
  • 2.4. Execution
• 3. Frontend
  • 3.1. Branch Prediction
  • 3.2. Decode
• 4. Backend
  • 4.1. Microcode
• 5. Memory
  • 5.1. Cache
    • 5.1.1. Hierarchy
    • 5.1.2. Placement Policy
    • 5.1.3. Management
  • 5.2. Memory Controller
    • 5.2.1. MMU
    • 5.2.2. TLB
• 6. Storage
• 7. Reference

1. Arithmetic

1.1. Integer

1.2. Real Numbers

Note that historically, floating point is not the only representation for real numbers, there were fixed point representations where the gaps are all of the same size

1.2.1. Fixed-point Representation

Proposed by William Kahan (Turing 1989), as an effort to design intel 8087.

1.2.2. Float Representation

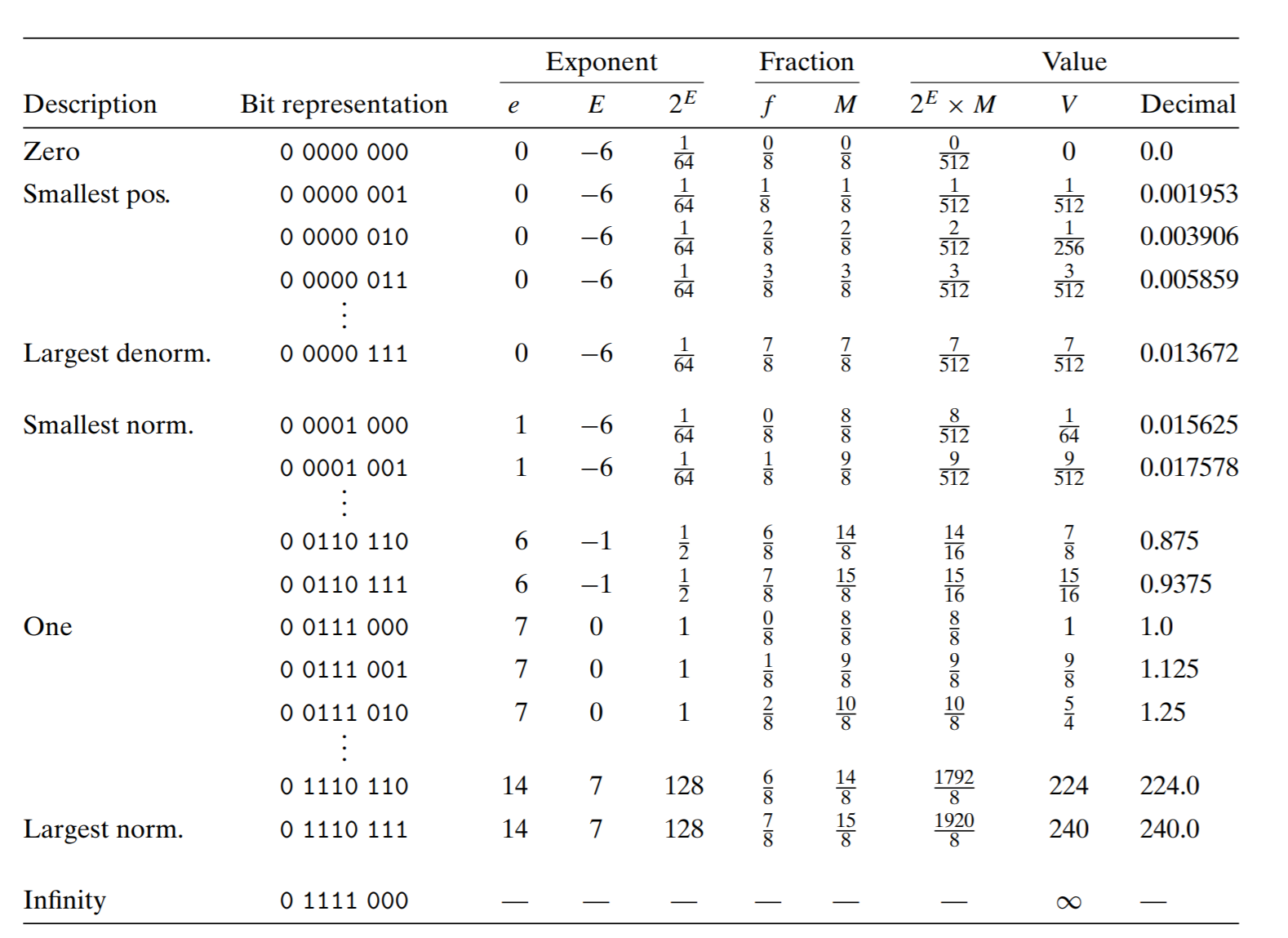
The IEEE 754 standard defines the representation of floating point as follows

\[(-1)^S (1+Fraction) \times 2^{(Exponent - Bias)}\]

The part of \(1+Fraction\) is also called significand, the fraction is also known as mantissa

Representations are different depending on the values of exponential

1. normalized case when exponent are not all zero or all one

\[(-1)^S (1.f_{n-1}f_{n-2}...f_{0}) \times 2^{(e_{k-1}e_{k-2}...e_{0} - Bias)}\]

where \(bias=2^{k-1}-1\)

2. denormalized case when exponent are all zero, then

\[(-1)^S (0.f_{n_1}f_{n-2}...f_{0}) \times 2^{1-Bias}\]

Notice both significant and exponent part have changed. This representation has a smooth transition from the denormalized case into normalized case. Additionally it provides a way to represent 0 (actually two way +0.0, -0.0 depending on the sign)

3. special case when exponent are all 1

• if fraction is 0, it is infinity
• otherwise fraction are nonzero, it is NaN

8 bit float number

exponent 4 bit, fraction 3 bit example from CSAPP

single-precision

float

• S is 1 bit
• Exponent is 8 bit and Bias is \(127_{Ten}\)
• Fraction is 24 bit (6 decimal digits of precision)
• range is around \([2.0 \times 10^{-38}, 2.0 \times 10^{38}]\)

var f float32 = 16777216  // 1<<24
fmt.Println(f == f+1)  // true

double-precision

In double-precision

• S is 1 bit
• Fraction is 11 bit and Bias is \(1023_{Ten}\)
• Fraction is 52 bit (15 decimal digits of precision)
• range is around \([2.0 \times 10^{-308}, 2.0 \times 10^{308}]\)

To find the detailed numbers on each machine, you can consult from standard C header.

1.2.2.1. Rounding

IEE754 use the Round-to-Even as the default mode.

• It in general rounds to the nearest number
• when the target is at the half of two numbers (e.g: \(XXX.YYY1000\)), then it rounds so that the least significant bit is even (0).

Other possible roundings are

• round toward zero
• round up
• round down

2. Processor

2.1. Notable CPU

• 4 bit: intel 4004 (first intel chip, 1970, 2k transistor)
• 8 bit: intel 8008 (1972, 3k transistors)
• 16 bit: intel 8086 (1976), PDP-11 (minicomputer DEC 1970)
• 32 bit: intel 80386 (1985), VAX-11 (DEC 1977)
• 64 bit

2.2. Flynn's taxonomy

2.2.1. SISD

pipelines

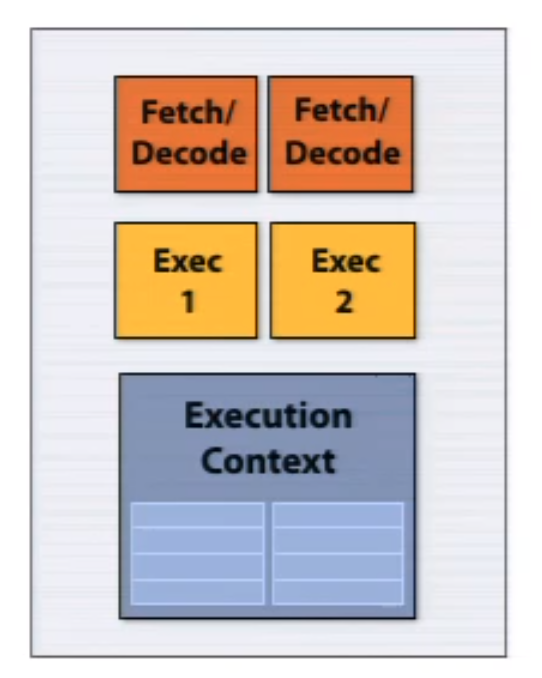
superscalar processor The superscalar architecture implements parallelism within one core executing independent part of instruction from the same instruction stream. This was one of the main strategies in the pre-multi core era, but requires a lot transistors for cache, branch predictor, out-of-order logics. P5 Pentium was the first x86 superscalar processor.

The following example shows a single-core architecture which can execute two independent instructions simultaneously from a single instruction stream.

2.2.2. SIMD

vector processor

instruction stream coherence: same instruction sequence applied to all elements, which is necessary for efficient SIMD execution, but not necessary for multicore parallelization

SSE instructions: 128 bit (4 wide float)

AVX instructions: 256 bits (8 wide float)

2.2.3. MISD

2.2.4. MIMD

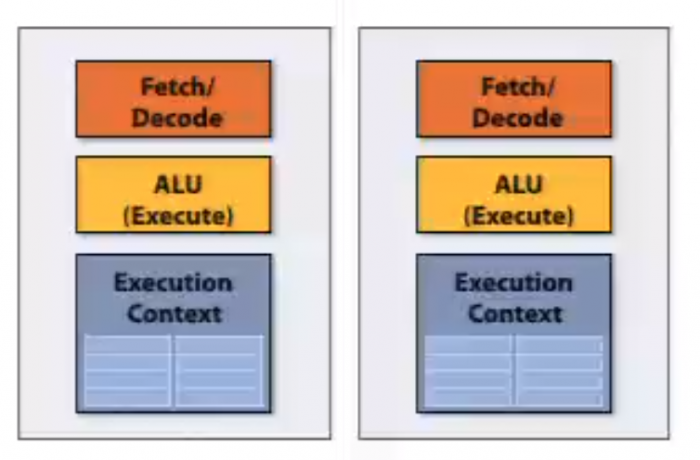
hyper-threading: super-scalar with multiple execution contexts in a single core

multi-core: thread-level parallelism. simultaneously execute a completely different instruction stream on each core

2.3. Pipeline

2.4. Execution

3. Frontend

Single-cycle implementation: an instruction is executed in one clock cycle, the slowest instruction decide cycle time

Multi-cycle implementation: instruction processing broken into multiple cycles/stages.

3.1. Branch Prediction

3.2. Decode

4. Backend

4.1. Microcode

5. Memory

5.1. Cache

Cache is usually implemented with SRAM

5.1.1. Hierarchy

• L1: reference 1ns, usually in core
• L2: reference 4ns, usually out core
• L3: usually shared by multiple cores

5.1.2. Placement Policy

• full associative cache: each memory can be placed anywhere
• directed mapped cache: each memory can be placed at one place
• LRU: Least Recently Used

5.1.3. Management

• Write-through: write data to cache and RAM at the same time
• Write-back: delay writing data to RAM

5.2. Memory Controller

5.2.1. MMU

the unit to translate virtual address into physical address

5.2.2. TLB

• the cache that saves the recent address mapping
• it is a cache of page tables
• only store the final translation even it is a multiple-level memory
• change cr3 in x86 can clear TLB automatically

6. Storage

7. Reference

[1] Patterson, David A., and John L. Hennessy. Computer Organization and Design ARM Edition: The Hardware Software Interface. Morgan kaufmann, 2016.

[2] Hennessy, John L., and David A. Patterson. Computer architecture: a quantitative approach. Elsevier, 2011.

[3] CMU 15-418/15-618: Parallel Computer Architecture and Programming

[4] CMU 18-447 Introduction to Computer Architecture

[5] CSAPP